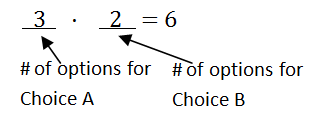Counting with Permutations and Combinations

 Combinatorics is a branch of mathematics that focuses on the study of finite or countable discrete structures. Combinatorics has applications in optimization, computer science, and statistical physics. There are times that it makes sense to count the number of ways an event could occur by looking at each possible outcome. However, when a large number of outcomes exists, this method becomes inefficient. If someone asked you how many possible regular license plates there are for the state of Oregon, it would not be feasible to count each and every one.

Instead, you could use the fact that on the typical Oregon license plate, there are 4 numbers and 3 letters. Using this information, about how many license plates could there be?

The Counting Principle

Consider choice A$\begin{array}{r}A\end{array}$ with 3 options (A1,A2,A3),$\begin{array}{r}(A_1,A_2,A_3),\end{array}$ and choice B$\begin{array}{r}B\end{array}$ with 2 options (B1,B2)$\begin{array}{r}(B_1,B_2)\end{array}$. If you had to choose an option from A$\begin{array}{r}A\end{array}$ and then an option from B$\begin{array}{r}B\end{array}$, the overall total number of options would be 3⋅2=6$\begin{array}{r}3\cdot 2=6\end{array}$. The options are A1B1,A1B2,A2B1,A2B2,A3B1,A3B2$\begin{array}{r}{A}_1{B}_1,A_1{B}_2,A_2{B}_1,A_2{B}_2,A_3{B}_1,A_3{B}_2\end{array}$.

You can see where the 6 comes from by making a decision tree and using the Fundamental Counting Principle. A decision tree is a graph that models the options possible at each stage of an experiment. To make a decision tree, you 1st need to determine how many decisions you are making. Here, there are only two decisions to make: 1) choose an option from A$\begin{array}{r}A\end{array}$, and 2) choose an option from B$\begin{array}{r}B\end{array}$, so you will have two "slots" in your decision tree. Next, think about how many possibilities there are for the 1st choice (in this case there are 3), and how many possibilities there are for the 2nd choice (in this case there are 2). The Fundamental Counting Principle says that you can multiply those numbers together to get the total number of outcomes.

[Figure 2]

The following video explains how to find the number of ways an event can occur:

 

Combinations and Permutations

Another type of counting question is when you have a given number of objects, you want to choose some (or all) of them, and you want to know how many ways there are to do this. For example, a teacher with a class of 30 students wants 5 of them to do a presentation, and she wants to know how many ways this could happen. These types of questions have to do with combinations and permutations. The difference between combinations and permutations is whether or not the order you are choosing the objects matters.

• A teacher choosing a group to make a presentation is a combination problem, because order does not matter.
• A teacher choosing 1st-, 2nd-, and 3rd-place winners in a science fair is a permutation problem, because the order does matter. (1st place and 2nd place are different outcomes.)

The factorial symbol, !, means to multiply every natural number up to and including that whole number together. For example, 5!=5⋅4⋅3⋅2⋅1$\begin{array}{r}5!=5\cdot 4\cdot 3\cdot 2\cdot 1\end{array}$. The factorial symbol is used in the formulas for permutations and combinations.

  Combination Formula

The number of ways to choose k$\begin{array}{r}k\end{array}$ objects from a group of n$\begin{array}{r}n\end{array}$ objects where order does not matter is 

nCk=(nk)=n!k!(n−k)!.$$\begin{array}{r}{}_n{C}_k={\displaystyle (\genfrac{}{}{0ex}{}{n}{k})}=\frac{n!}{k!\left(n-k\right)!}.\end{array}$$

The following video introduces combinations and explains how to evaluate combinations and solve counting problems using combinations: 

 

Play, Learn, and Explore with Combinations: Friends at a Party

 

  Permutation Formula

The number of ways to choose and arrange k$\begin{array}{r}k\end{array}$ objects from a group of n$\begin{array}{r}n\end{array}$ objects is

nPk=k!(nk)=k!⋅n!k!(n−k)!=n!(n−k)!.$$\begin{array}{r}{}_n{P}_k=k!{\displaystyle (\genfrac{}{}{0ex}{}{n}{k})}=k!\cdot \frac{n!}{k!\left(n-k\right)!}=\frac{n!}{\left(n-k\right)!}.\end{array}$$

The following video explains how to evaluate factorials, use permutations to solve problems, and determine the number of permutations with indistinguishable items: 

Play, Learn, and Explore with Permutations: Podiums

Notice that in both combination and permutation problems, you are not allowed to repeat your choices. Any time you are allowed to repeat and order does not matter, you can use the Fundamental Counting Principle. (Problems with repetition where order does not matter are more complex and not discussed in this section.)

Whenever you do a counting problem, the 1st thing you should decide is whether the problem is a Fundamental Counting Principle problem, a permutation problem, or a combination problem. You'll find that permutation problems can also be solved with the Fundamental Counting Principle, but the opposite is not true. There are many Fundamental Counting Principle problems (ones where you are allowed to repeat choices) that cannot be solved with the permutation formula.

Examples

Example 1

You are going on a road trip with 4 friends in a car that fits 5 people. How many different ways can everyone sit if you have to drive the whole way?

Solution:

The Fundamental Counting Principle is a great way of thinking about this problem. You have to sit in the driver's seat. There are 4 options for the 1st passenger seat. Once that person is seated, there are 3 options for the next passenger seat. This goes on until there is one person left with 1 seat.

1⋅4⋅3⋅2⋅1=24$$\begin{array}{r}1\cdot 4\cdot 3\cdot 2\cdot 1=24\end{array}$$

Example 2

How many different ways can the gold, silver, and bronze medals be awarded in an Olympic event with 12 athletes competing?

Solution:

Since the order does matter with the 3 medals, this is a permutation problem. You will start with 12 athletes and then choose and arrange 3 different winners.

12P3=12!(12−3)!=12!9!=12⋅11⋅10⋅9⋅…9⋅…=12⋅11⋅10=1,320$$\begin{array}{r}{}_{12}{P}_3=\frac{12!}{\left(12-3\right)!}=\frac{12!}{9!}=\frac{12\cdot 11\cdot 10\cdot 9\cdot \dots }{9\cdot \dots }=12\cdot 11\cdot 10=1,320\end{array}$$

Note that you can also use the Fundamental Counting Principle to decide how many possibilities are there for gold (12), how many possibilities are there for silver (11, since one already has gold), and how many possibilities are there for bronze (10). You can use the Fundamental Counting Principle for any permutation problem.

12⋅11⋅10=1,320$$\begin{array}{r}12\cdot 11\cdot 10=1,320\end{array}$$

Example 3

You are deciding which awards you are going to display in your room. You have 8 awards, but you only have room to display 4 awards. Right now you are not worrying about how to arrange the awards, so the order does not matter. How many ways could you choose the 4 awards to display?

Solution:

Since order does not matter, this is a combination problem. You start with 8 awards and then choose 4.

8C4=(84)=8!4!(8−4)!=8⋅7⋅6⋅54⋅3⋅2⋅1=7⋅2⋅5=70$$\begin{array}{r}{}_8{C}_4={\displaystyle (\genfrac{}{}{0ex}{}{8}{4})}=\frac{8!}{4!\left(8-4\right)!}=\frac{8\cdot 7\cdot 6\cdot 5}{4\cdot 3\cdot 2\cdot 1}=7\cdot 2\cdot 5=70\end{array}$$

Note that if you try to use the Fundamental Counting Principle with this question, you will need to do an extra step of reasoning. There are 8 options you could choose 1st, then 7 left, then 6, and lastly 5.

8⋅7⋅6⋅5=1,680$$\begin{array}{r}8\cdot 7\cdot 6\cdot 5=1,680\end{array}$$

This number is so big because it takes order into account, which you don't care about. It is the same result you would get if you used the permutation formula instead of the combination formula. To get the right answer, you need to divide this number by the number of ways 4 objects can be arranged, which is 4!=24$\begin{array}{r}4!=24\end{array}$. This has to do with the connection between the combination formula and the permutation formula.

Example 4

Recall the problem from the Introduction: How many Oregon license plates could be created with 3 letters and 4 numbers?

Solution:

A license plate that has 3 letters and 4 numbers can be represented by the Fundamental Counting Principle with 7 spaces. You can use the Fundamental Counting Principle because order definitely does matter with license plates. The 1st spot is a number, the next three spots are letters, and the last three spots are numbers. Note that when choosing a license plate, repetition is allowed.

10⋅26⋅26⋅26⋅10⋅10⋅10=263⋅104=175,760,000$$\begin{array}{r}10\cdot 26\cdot 26\cdot 26\cdot 10\cdot 10\cdot 10={26}^3\cdot {10}^4=175,760,000\end{array}$$

This number is only approximate because, in reality, certain letter and number combinations are not allowed, some license plates have extra symbols, and some commercial and government license plates have more numbers, fewer letters, or blank spaces.

Example 5

There are 20 hockey players on a pro NHL team, 2 of whom are goalies. How many sets of 5 skaters and 1 goalie can be on the ice at the same time?

Solution:

The question asks for how many on the ice, implying that order does not matter. This is combination problem with 2 combinations. You need to choose 1 goalie out of a possible of 2, and choose 5 skaters out of a possible 18.

(21)(185)=2⋅18!5!⋅13!=17,136$$\begin{array}{r}{\displaystyle (\genfrac{}{}{0ex}{}{2}{1})}{\displaystyle (\genfrac{}{}{0ex}{}{18}{5})}=2\cdot \frac{18!}{5!\cdot 13!}=17,136\end{array}$$

Example 6

How many different ways could you score a 70% on a 10-question test, where each question is weighted equally and is either right or wrong?

Solution:

The order of the questions you got right does not matter, so this is a combination problem.

(107)=10!7!3!=120$$\begin{array}{r}{\displaystyle (\genfrac{}{}{0ex}{}{10}{7})}=\frac{10!}{7!3!}=120\end{array}$$

Example 7

How many different 4-digit ATM passwords are there? Assume you can repeat digits.

Solution:

Order does matter. There are 10 digits, and repetition is allowed. You can use the Fundamental Counting Principle for each of the 4 options.

10⋅10⋅10⋅10=10,000$$\begin{array}{r}10\cdot 10\cdot 10\cdot 10=10,000\end{array}$$

Summary

• The Fundamental Counting Principle states that if one event has m possible outcomes and a 2nd event has n possible outcomes, then there are m⋅n$\begin{array}{r}m\cdot n\end{array}$ total possible outcomes for the two events together.
• A combination is the number of ways of choosing k$\begin{array}{r}k\end{array}$ objects from a total of n$\begin{array}{r}n\end{array}$ objects (order does not matter). 
  nCk=(nk)=n!k!(n−k)!$$\begin{array}{r}{}_n{C}_k={\displaystyle (\genfrac{}{}{0ex}{}{n}{k})}=\frac{n!}{k!\left(n-k\right)!}\end{array}$$
• A permutation is the number of ways of choosing and arranging k$\begin{array}{r}k\end{array}$ objects from a total of n$\begin{array}{r}n\end{array}$ objects (order does matter). 
  nPk=k!(nk)=k!⋅n!k!(n−k)!=n!(n−k)!